Fat-Tailed Probability Distributions

Get an understanding of the real-world effects of Fat-Tailed distributions - and how to use them to your advantage.

Oct 22, 2022

What they are, where to find them & which side dishes they should be enjoyed with

Fat-tailed probability distributions describe random variables that can produce a small number of huge values. Most values values will be small but a handful will be huge. The best examples are the Pareto and the Cauchy, t-distribution with one degree of freedom.

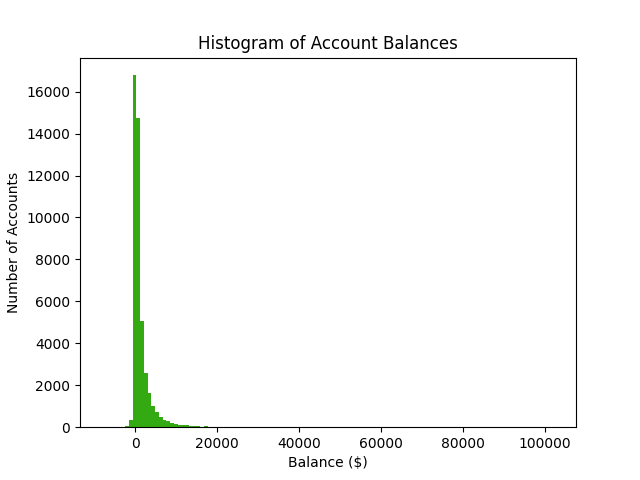
You might be wondering what I mean by huge or extreme values. Consider the bank account balance example from a previous learning python article. Most customers had account balances near zero. The largest account balance was $102,127. The second largest account balance was only $32,892. Wealth is an excellent example of fat-tailed distributions. Most people only have a small amount of assets. A very small amount of people have a huge net-worth.

In stark contrast to fat-tailed distributions, is the Normal distribution. My previous article mentions how Normal distributions occur when we have lots of small and unbiased deviations. In a Normal distribution, 99.9% of all values are within three standard deviations. A Normal distribution produces small deviations. Although extreme values are theoretically possible, they are extremely unlikely - practically impossible. A fat-tailed distribution produces many tiny deviations and a handful of huge deviations. Extreme values are also reasonably unlikely in fat-tailed distributions, they are just likely enough to occur 1% of the time.

The fat tailed world has an interesting behaviour that you should know about

Imagine a huge amount of money, let’s call it $XXX. In a fat-tailed world, you are more likely to earn $XXX from a single event than from two events. In a thin-tailed world, you are more likely to earn $XXX as the sum of two events. Keep this in mind when you read the section on how fat-tailed distributions relate to your career.

A potential underlying cause of the fat tailed effect

Unobserved information can be an underlying cause of the fat tailed effect. Imagine the share price of a publicly listed utility company. Being an established company, imagine that someone decided that it was acceptable to use a Gaussian distribution to model the daily percentage returns of the stock price. This “model” would be fine for some time. One day, news breaks that the financial reports of the company have been falsified for several years and the company is actually bankrupt. The price of the stock crashes to zero. According the Gaussian model, this is a once-in-a-gazillion-years type of event. However, events of this nature have happened several times in real financial markets.

Let’s take a step back and consider a scenario where the price of the stock had been trending up prior to its collapse. Imagine that our analyst fit a beautiful regression model to predict the percentage returns of the stock price - before the crash. The independent variables, X, include all sorts of wonderful variables such as inflation, GDP, population, predicted price of gas, …etc. Our analyst fits this model and shows us the the errors are Normally distributed.

However, one important variable missing. An indicator variable. The value of this variable is 1 when the fraud is discovered, otherwise it is 0. Initially, the missing variable doesn’t have any impact on the model - until it does.

A properly specified regression model should have normally distributed errors because the errors are made up of small, unbiased disturbances. When you are missing a variable that occasionally makes a big difference, then the central limit theorem no longer holds. You might also be thinking about the omitted variable bias, where coefficients are biased because variables are omitted.

Imagine that you are building a real estate automated valuation model. You are building a model to predict how much any house is likely to sell for

How it relates to data science projects

Some data science projects aim to predict tail events. Perhaps someone decides that fancy “machine learning” can predict something that human discretion cannot. In order for this to work, you need to have features that measure something related to these tail events. In the listed company example above, investors could not tell that the company’s accounts were fraudulent by just viewing the publicly available information.

How long a data science project will take, how much it will cost and whether it is possible at all

How it relates to career guidance in general

Professional Data Science

Discussion about this post